How many rounds does the small circle rotate?

Today I came across a very interesting problem: suppose a small circle with radius 1 is rolling on a big circle with radius 2, how many rounds does the small circle rotate when it rolls around the big circle once? Being told the correct answer is 3, I am confused as I am unable to figure it out. Therefore, I wrote a program to simulate the scenario.

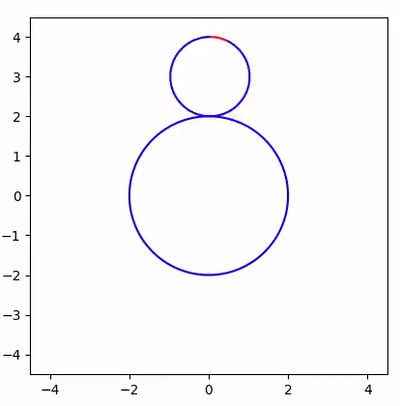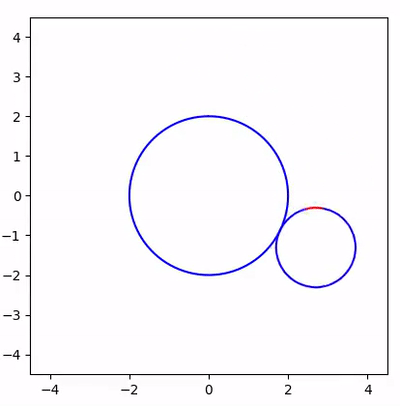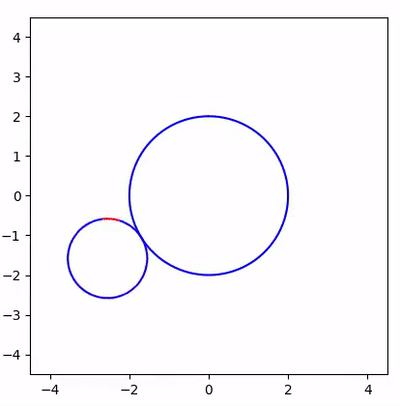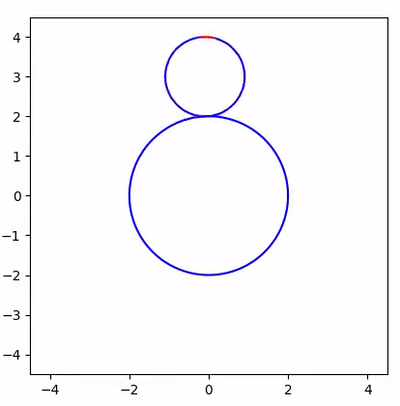
The design of the simulation

As it is illustrated below, the big circle and the small circle are approximated by a \(2n\)-polygon and a \(n\)-polygon, respectively. The rolling motion is simply rotating the \(n\)-polygon by \(\theta\) with respect to the intersection on the right. The value of \(\theta\) can be computed rather easily since we know the coordinates of all points in the figure.

Why 3 instead of 2?

If we simplify the problem to a triangle rolling on a hexagon, the explanation is straightforward. Since the circumference of the triangle (small circle) is half of the circumference of the hexagon (big circle), every side of the triangle needs to touch some sides of the hexagon twice. This is how the number 2 comes from. However, when we consider an arbitrary vertex of the triangle, it can be seen that it only needs two rolling motions to rotate one round! Traversing across the hexagon needs 6 rolling motions, which means the triangle needs to rotate 3 rounds. This conclusion can be generalized to \(n\)-polygons.

Source code

The source code can be found here.